Critical Difference: What is a meaningful change in our data?
When exploring trends in children’s development, the broad question that we want to answer is: “Are our kindergarten-aged children doing better, worse, or about the same as in the past?” and is that change in fact a meaningful change? HELP has developed a method that communities and stakeholder groups can use to make informed judgements about change over time in EDI scores. The method that HELP has used to examine ‘change over time’ is described in the literature as Critical Difference.
On this page, you will find information about Critical Difference, how to calculate it and a calculator to help you do so. We have also prepared a detailed research brief on the topic.
What is Critical Difference?
A Critical Difference is the amount of change over time in a neighbourhood’s EDI vulnerability rate that is large enough to be considered a meaningful change. By meaningful, we mean worthy of further discussion and exploration. We use statistical significance as a minimum requirement for considering a change to be meaningful, as this reflects a high likelihood that the vulnerability rate has truly shifted. In other words, there is a low likelihood that the observed change over time is due to either differences in how teachers rated students (i.e., measurement issues) or something about participation rates (i.e., sampling issues).
The critical difference methodology is most often used to assess change over time at the HELP neighbourhood level, but it is not restricted to that level. It could be used, for example, at larger aggregations such as communities, school districts, or local health areas. Alternatively, it is also possible to focus on smaller aggregations, such as schools. However, this is rarely advisable, given the small number of Kindergarten children at this level of aggregation. As discussed below, small numbers require much larger differences in vulnerability over time to be considered meaningful.
Besides using Critical Difference to assess change over time for one neighbourhood (or other aggregation), it can also be used to assess whether two neighbourhoods, during the same time period, have meaningfully different EDI vulnerability rates. The methodology is the same, with one provision – the two neighbourhoods (or other geographic units) need to be at the same level of aggregation. It is not appropriate, for example, to compare a HELP neighbourhood with its school district, or a school district with the province as a whole. It is also not appropriate to use it to calculate change over time for 3 places or 3 points in time.
Critical Difference Calculator
To make calculating critical differences easier we have created the Critical Difference Calculator, a tool that will help with interpreting change over time and differences between EDI scores in the BC context.
To use the calculator, simply select the scale for the data you are using, enter the values for each place or time and click on the Calculate button. The result will be calculated automatically. More detailed information on how to use the calculator including examples can be found below.
How to Calculate Critical Difference
Example 1.Comparing EDI scores across time in one neighbourhood
Neighbourhood ‘A’ had a vulnerability rate on ‘one or more scales’ of 34% in Wave 2, based on scores for 52 children. In Wave 8, the vulnerability rate dropped to 26%, based on scores for 63 children.
Using the critical difference equation for ‘vulnerable on one or more scales’, or by using the critical difference calculator above, the critical difference value can be determined. The critical difference turn out to be 10 percentage points in the first time period, and 9 points in the second time period. We then calculate the average critical difference, which is 9.5 percentage points. Since the average critical difference is larger than the observed drop of 8 percentage points (34% to 26%), we conclude that the vulnerability rate has not changed enough to be considered a meaningful or significant difference.
Example 2. Comparing EDI scores across neighbourhoods.
Neighbourhood ‘A’ has a vulnerability rate on ‘one or more scales’ of 34% in Wave 8, based on scores for 52 children. Neighbourhood B has a vulnerability rate of 16% in Wave 8, based on scores for 310 children. The same critical difference equations apply as in Example 1. For Neighbourhood ‘A’, the critical difference is 10 percentage points. For Neighbourhood ‘B’, it is 4 percentage points. The average critical difference is 7 percentage points. Since this is smaller than the observed difference between the neighbourhoods of 18 percentage points, Neighbourhood ‘B’s lower vulnerability rate is considered to be significantly different than Neighbourhood ‘A’s.
How are Critical Difference equations produced?
Micro-simulation techniques are used to produce the critical difference equations. In the simulations, the effects on uncertainty of different sources of measurement error are tested, such as neighbourhood size and teacher effects (including leniency and consistency of scoring). For each combination of neighbourhood size and teacher-related measurement error, the uncertainty of the vulnerability rate was then calculated. The critical difference equations and associated curves show how uncertainty changes with neighbourhood size, assuming a moderate level of teacher effects.
| Scale | Equation |
|---|---|
| Physical | y=56.532x-0.469 |
| Social | y=34.702x-0.455 |
| Emotional | y= 46.657x-0.488 |
| Language | y=52.987x-0.521 |
| Communication | y=52.539x-0.487 |
| One or More Scales | y=73.941x-0.507 |
x = number of children in area of interest (or average number of children if the count is different between time periods or areas that are being compared)
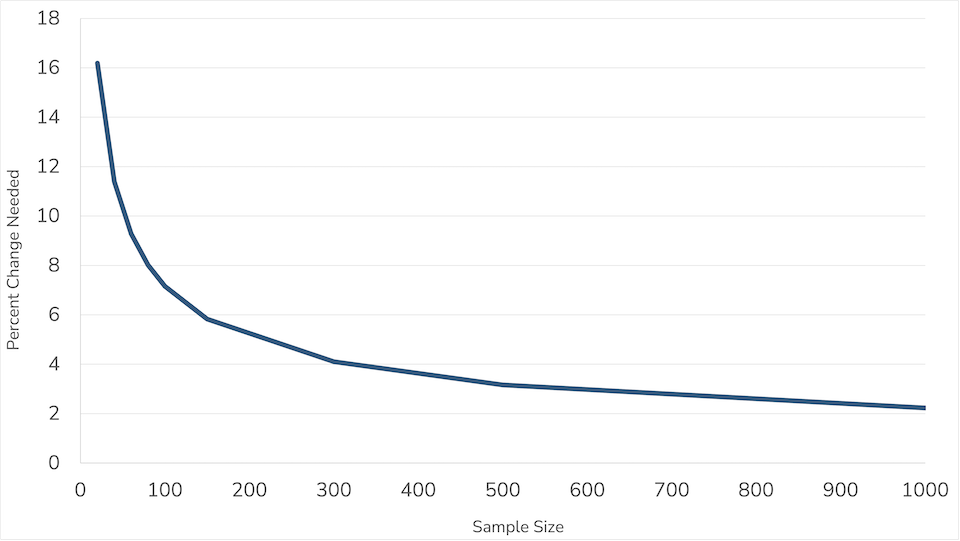
Power Curves
Vulnerability rates for large populations are more precise, critical difference values are lower and therefore the percentage change needed for it to be deemed a meaningful change is smaller. Smaller populations have higher critical difference values and require a larger percentage change in vulnerability rates for the change to be considered meaningful. For all EDI scales, the critical difference value of the curve does not decrease after the number of children exceeds 1,250; this is the limit placed on critical difference, regardless of group size. Having a cutoff is necessary to avoid situations where a very small change in vulnerability over time results in a critical difference, due only to very large numbers of children.
Measuring Uncertainty
When an EDI vulnerability rate is calculated for a neighbourhood, school district or some other geographic unit, there is always some uncertainty about what the true vulnerability rate actually is. There are two main sources of uncertainty, relating to issues of sampling and measurement.
Sampling Uncertainty
On average, for each EDI wave, provincial participation rates are in the range of 85% to 95%, with variation between school districts. In some neighbourhoods this sample might not be representative of the population as a whole. This is because, though the EDI is administered in almost all public schools, few private schools and on-reserve schools have participated in the EDI.
Measurement Uncertainty
Uncertainty related to measurement is common for all tools that measure complex constructs, such as health, well-being, or social status. Similarly, the EDI measures complex qualities such as social competence and emotional maturity. We accept that the EDI items we use to capture these domains cannot completely represent their actual complexity, resulting in some measurement error.
In the case of the EDI, there is a second measurement-related source of uncertainty: variability in how teachers interpret EDI items when rating their students. For example, teachers may differ in how lenient or severe they are in their EDI scoring, or may differ in how consistent they are in their scoring. HELP takes a number of steps to minimize this teacher-related uncertainty.
As HELP administers the EDI questionnaire each year, we work in constant collaboration with schools and teachers to facilitate the data gathering process and to ensure that we have high quality, reliable data on children. Annually, we invest in a standardized training package for kindergarten teachers. This package provides information on the background and use of the EDI, along with detailed instructions on EDI completion. We also have specific training content to address potential teacher bias. Our goal is to standardize the administration and interpretation of the EDI items as much as possible. However, over the hundreds of kindergarten teachers who complete the EDI for each wave of provincial data collection, some between-teacher differences are bound to persist.
Both sampling-related and measurement-related uncertainty in EDI vulnerability rates are affected by the number of children in the population (e.g.,neighbourhood, school district). For statistical reasons, uncertainty inevitably gets smaller as the population size gets larger. As seen in the power curve graph below, vulnerability rates for larger populations are more precise (i.e., critical difference values are lower) than for smaller populations.